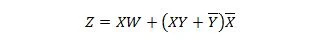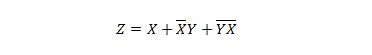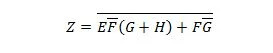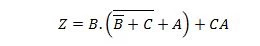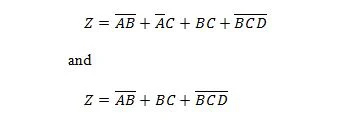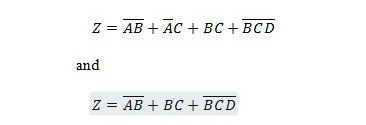第 2 章: ブール代数とそれに関連するコンピュータ コンポーネント
2.1 基本的なブール演算子
私（著者）は背が高く、あなた（読者）も背が高いと仮定します。誰かがあなたに私たち二人とも背が高いかと尋ねたら、あなたは「はい」（本当です）と答えるでしょう。もし彼が私たち二人とも背が低いのかと尋ねたら、あなたは「いいえ」と答えるでしょう（偽）。あなたが背が低くて、私が背が高いとすると、彼があなたか私のどちらかが背が高いかと尋ねたら、あなたの答えは「はい」（本当）でしょう。もし彼があなたも私も背が高いかと尋ねたら、あなたは答えられないでしょう。最後の質問はするべきではない、あるいはその質問には答えがない、とさらに言うかもしれません。さて、あなた（読者）に知っておいていただきたいのは、今日、特定の状況下では、この質問をする必要があるということです。
生物学では、人は背が高いか低いかのどちらかです。その人が中身長になるのは「環境」条件です。科学者の一人、ジョージ・ブールは、この種の質問に対する一連の答えまたはルールを定義しました。このルールは、オンライン キャリア コース (章) のこのセクションで学習します。これらのルールは、今日のコンピューティング、プログラミング、エレクトロニクス、電気通信で使用されています。実際、これらのルールがなければ、今日では一般的になっているように、コンピューターを所有することはできません。今日では一般的となっているように、プログラミングもできないでしょう。
正しいか間違っているか
単純な人間の言語のステートメントは、それ自体が真か偽のいずれかです。私が「私は背が高い」と言った場合、それは本当か嘘かのどちらかです。私が「あなたは背が高いです」と言った場合、それは本当か嘘かのどちらかです。私が背が高くて、あなたが背が低い場合、あなたも私も背が高いかどうかという質問がなされた場合、ブール論理では、真か偽の答えが与えられなければなりません。この2つのうちどちらを与えるべきでしょうか？ブール氏はこの質問に実際には答えなかった。彼は単に私たちが従うべき一連のルールを考え出しただけです。幸いなことに、これらのルールを正しい文脈で従えば、あいまいさはまったくありません。これらのルールのおかげで、今日私たちはコンピューターとプログラミングを使用することができます。ルールは今あなたに与えられています。ルールは実際には説明できません。あなたはただそれらを受け入れるだけです。ルールは、AND、OR、NOT の 3 つの見出しの下にあります。
そして
あなたも私も背が高いかどうかという質問ができます。私の身長とあなたの身長は、AND ルールのセットによって結合されます。従うべき AND ルールは次のとおりです。
false AND false = false
false AND true = false
true AND false = false
true AND true = true
さて、背が高いのが真、背が低いのが偽であるとします。これは、私が背が低くて、あなたも背が低い場合、あなたも私も背が低いことを意味します。私が背が低くて、あなたが背が高いなら、あなたも私も背が低いことになります。それがブール値の答えであり、受け入れる必要があります。もし私が背が高くてあなたが背が低いなら、あなたも私も背が低いことになります。私が背が高くて、あなたも背が高いなら、あなたも私も背が高いです。これらはすべて AND ブール値のルールであり、読者 (読者) は受け入れる必要があります。
または
あなたまたは私が背が高いかどうかという質問をすることができます。私の身長とあなたの身長は、OR ルールのセットによって結合されます。従うべき OR ルールは次のとおりです。
false または false = false
false OR true = true
true または false = true
true OR true = true
繰り返しますが、背が高いのが真、背が低いのが偽であるとします。これは、私が背が低い、またはあなたが背が低い場合、あなたまたは私が背が低いことを意味します。私が背が低い、またはあなたが背が高い場合、あなたまたは私は背が高いです。私が背が高い、またはあなたが背が低い場合、あなたまたは私は背が高いです。私が背が高い、またはあなたが背が高い場合、あなたまたは私は背が高いです。これらはすべて、受け入れる必要があるブール ルールです。
ない
さて、ブール論理では、2 つの状態 (可能な答え) のみが存在します。つまり、身長が高くなければ、背が低いということです。背が低くなければ、背は高いです。他には何もありません。以下は従うべきではないルールです。
偽ではない = 真
真ではない = 偽
伸ばす（引く）ことができる紐（またはバネ）があるとします。弦が自然な状態にあるときに、私が「短くない」と言えば、弦を伸ばすことになります。それが解釈です。文字列が伸びているときに、私が「長くない」と言えば、文字列が縮むことを許可することになります。それが解釈です。
与えられたルールをさまざまなカテゴリーに分けてすべて暗記する必要があります。
3 つ以上のオペランド
コンピュータ言語では、AND、OR、NOT をそれぞれ演算子と呼びます。 NOT 演算子の場合、答えを得るために必要なオペランド (演算子の値) は 1 つだけです。 AND または OR 演算子の場合は、3 つ以上のオペランドを指定できます。前の例では、AND と OR の 2 つのオペランドを示しています。次のように、AND には 3 つのオペランドを指定できます。
偽 AND 偽 AND 偽 = 偽
false AND false AND true = false
これらは 2 行です。それぞれに 2 つの AND 演算子があります。オペランドが 3 の場合、実際には 9 行になります。 AND 演算子の場合、最後の行 (9 行目) のみが true と等しくなります。前の行はすべて false です。 AND の 2 つのオペランドでは、最後の行のみが真となることに注意してください。前の 3 行はすべて false です。オペランドが 4 つの場合、行は 16 行あり、AND 演算子に当てはまるのは最後の行だけです。
AND のパターンと OR のパターンは異なります。 2 つの OR 演算子に 3 つのオペランドがあるため、行も 9 行あり、今回は最初の行だけが false になります。 2 行目から 9 行目までが true です。 OR の 2 つのオペランドでは、最初の行のみが true になることに注意してください。残りの 3 行はすべて false です。 OR のオペランドが 4 つの場合、行数も 16 になります。
NOT 演算子は 1 つのオペランドのみを扱います。 NOT false は true、NOT true は false です。
2.2 2 オペランド真理値表とその電子部品
数学には代数という科目があります。そのほんの一部は前の章で見られました。代数の一種にブール代数というものがあります。ブール代数では、真は基数 2 桁の 1 によって識別され、偽は基数 2 桁の 0 によって識別されます。
コンピュータユニットの内部コンポーネントは電子部品です。コンピュータ システムのシステム ユニットにはデジタル電子コンポーネントが搭載されています。 AND 演算は、AND ゲートと呼ばれる小さな電子部品によって実行されます。 OR 演算は、OR ゲートと呼ばれる小さな電子部品によって実行されます。 NOT演算はNOTゲートと呼ばれる小さな電子部品によって行われます。集積回路 (IC) チップ内にこれらのゲートが多すぎる場合があります。
AND 真理値表とそのゲート
次の表は、AND 真理値表とその AND ゲート (小規模回路) シンボルを示しています。
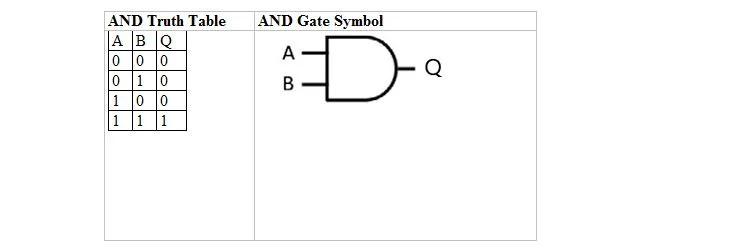
AND 真理値表とそのゲートの両方において、A と B は 2 つの入力変数です。 Q は出力変数です。 A は 1 または 0 です。B は 1 または 0 です。Q は 1 または 0 です。1 と 0 を含む AND 真理値表は、前の true/false AND 真理値レイアウト (表) と同じです。 AND 式は次のとおりです。
Ａ． B = Q
ここで、ドット (.) は AND (ブール値) を意味します。ドットを省略すると、AB = Q となり、同じことを意味します (AND)。
注: 4 行の A と B のビットは、ペアとして、0 (または 00) から始まる 2 進数の最初の 4 つの数値、つまり 00、01、10、11 です。
次の表は、OR 真理値表とその OR ゲート (小規模回路) シンボルを示しています。
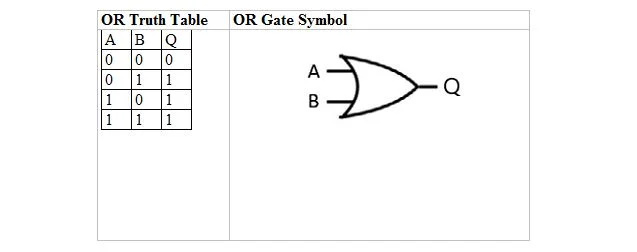
OR 真理値表とそのゲートの両方において、A と B は 2 つの入力変数です。 Q は出力変数です。 1 と 0 の OR 真理値表は、前の true/false OR 真理値のレイアウト (表) と同じです。
OR 方程式は次のとおりです。
A + B = Q
ここでの + は加算ではなくブール OR を意味します。この方程式は「A または B が Q に等しい」と読み取られます。
次の表は、NOT 真理値表とその NOT ゲート (小規模回路) シンボルを示しています。
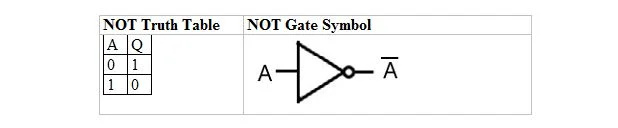
NOT 真理値表または NOT ゲートには、入力と出力が 1 つだけあります。入力が 0 の場合、出力は 1 です。入力が 1 の場合、出力は 0 です。NOT ゲートは一種の反転を行います。出力変数は入力変数と同じですが、バー (上線) が付いています。 1 と 0 からなる NOT 真理値表は、前の true/false OR 真理値のレイアウト (表) と同じです。
NOT 方程式は次のとおりです。
A = Q
ここで、Q = A であり、A の上のバーは補数を意味します。 0 の補数は 1 で、1 の補数は 0 です。NOT ゲートは INVERTING ゲートとも呼ばれます。
これらは、デジタル エレクトロニクス (ブール代数を使用) における基本 (またはルート) 真理値表とそのゲート (小さな回路) です。次の図に示されている他の 3 つの真理値表とそのゲートは便宜上のものであり、前の 3 つの真理値表に基づいています。
AND真理値表とゲートから導出される真理値表とゲートがあります。それらは、NAND (NOT AND) 真理値表および対応する NAND ゲートと呼ばれます。 NAND 真理値表とその NAND ゲートは次のとおりです。
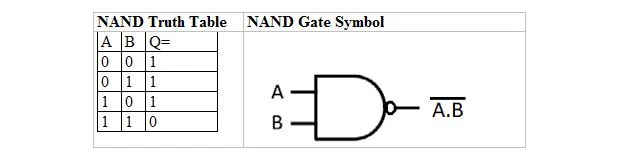
NAND 真理値表を取得するには、AND 真理値表の出力に移動し、各桁をその補数に置き換えます。 0 の補数は 1 で、1 の補数は 0 です。NAND ゲートは AND ゲートと似ていますが、出力ラインの前に小さな円があります。 NAND の方程式は次のとおりです。
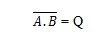
ここで、「A」と「B」の結果の補数を意味します。バー (オーバーライン) は、ゲート内の小さな円で表されます。 A と B の間のドットは省略できることに注意してください。
OR 真理値表とゲートから派生する別の真理値表とゲートがあります。それらは、NOR (NOT OR) 真理値表および対応する NOR ゲートと呼ばれます。 NOR 真理値表とその NOR ゲートは次のとおりです。
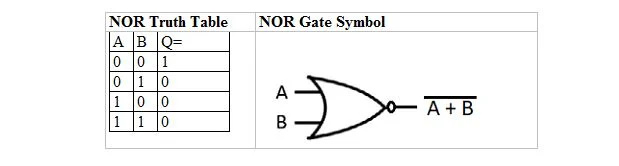
NOR 真理値表を取得するには、OR 真理値表の出力に移動し、各桁をその補数で置き換えます。 0 の補数は 1 で、1 の補数は 0 です。NOR ゲートは OR ゲートと似ていますが、出力ラインの前に小さな円があります。 NOR 方程式は次のとおりです。
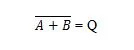
どこ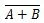 
「A」または「B」の結果の補数を意味します。バー (上線) はゲート内の小さな円で表されます。
排他的論理和 (XOR)
OR ゲートの真理値表は次のとおりです。
通常の英語では、1 OR 1 の最後の行が 1 になるのか 0 になるのかは明確ではありません。そのため、ブール代数には 2 種類の OR 真理値表と、対応する 2 つのゲートがあります。通常の OR では、1 OR 1 の最後の行は 1 になります。もう 1 つのタイプの OR は排他的 OR (XOR) で、最初の 3 行は通常の OR (出力を含む) の最初の 3 行と同じです。ただし、最後の 4 行目では、1 OR 1 は 0 になります。
次の表に、XOR 真理値表とその XOR ゲート (小規模回路) シンボルを示します。
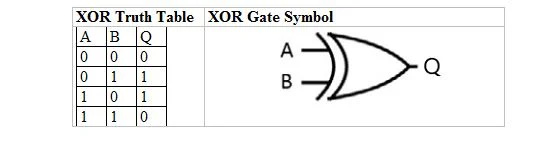
XOR 真理値表とそのゲートの両方において、「A」と「B」は 2 つの入力変数です。 「Q」は出力変数です。
XOR 式は次のとおりです。
A ⊕ B = Q
ここでの ⊕ はブール XOR を意味します。
通常の OR は、いずれかまたは両方を意味します。排他的論理和は厳密に意味します どちらか 両方ではありません。
2.3 ブール仮説
仮説は、特定の結論が導き出される前提条件です。 AND、OR、NOT 方程式 (真理値表) に基づいた 10 のブール公準があります。これらの方程式は関数とも呼ばれます。基本的な関数は次のように再コピーされます。
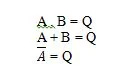
これらはブール代数の基本的な関数 (方程式) です。次の他の 3 つの (関数) 方程式は基本関数ではありません。
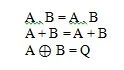
ここでの最後の関数は特殊ですが、基本的な関数とはみなされません。
ブール公準は次のとおりです。
AND関数から
1) 0 。 0 = 0
二十。 1 = 0
3) 1. 0 = 0
４）１． 1 = 1
OR関数から
5) 0 + 0 = 0
6) 0 + 1 = 1
7) 1 + 0 = 1
8) 1 + 1 = 1
NOT関数から
9) 0 = 1
10) 1 = 0
注記： これらの公準は、独立した方法で表現される AND、OR、および NOT 真理値表の行にすぎません。読者は与えられた仮定を暗記する必要があります。
2.4 ブール値のプロパティ
プロパティは何かの特性のようなものです。ブール プロパティは、ブール公準から導出される方程式です。このセクションでは、プロパティは導出せずに単に与えられ、後で使用されます。次の 25 個のプロパティが 10 の見出しの下にグループ化されています。
AND 関数のプロパティ
プロパティ 1:
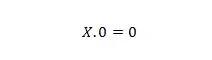
ここで、X は 1 または 0 です。これは、X が何であっても、結果は常に 0 になることを意味します。
注: 変数は、必ずしも A、B、C、または D である必要はありません。変数は、W、X、Y、Z、またはその他の文字にすることができます。
プロパティ 2:
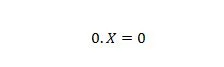
X は 1 または 0 です。プロパティ 1 とプロパティ 2 の違いは、両方の方程式の等号の左側で、X と 0 の位置が入れ替わることに注意してください。
特性 3:
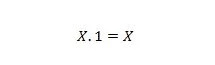
X が 0 の場合、0.1 = 0。X が 1 の場合、1.1 = 1。
特性 4:
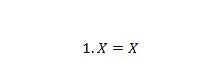
X が 0 の場合、1.0 = 0。X が 1 の場合、1.1 = 1。プロパティ 3 とプロパティ 4 の違いは、両方の方程式の左側で、 X と 1 が入れ替わります。
OR 関数のプロパティ
特性 5:
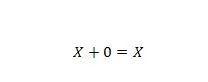
ここで、X は 1 または 0 です。つまり、X が 0 の場合、結果は 0 になります。X が 1 の場合、結果は 1 になります。
特性 6:
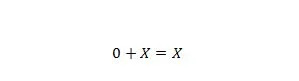
X は 1 または 0 です。プロパティ 5 とプロパティ 6 の違いは、両方の方程式の左側で X と 0 の位置が入れ替わることに注意してください。
特性 7:
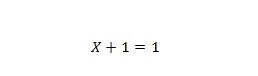
X が 0 の場合、0 + 1 = 1。X が 1 の場合、1 + 1 = 1。
特性 8:
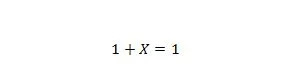
X が 0 の場合、1 + 0 = 1。X が 1 の場合、1 + 1 = 1。プロパティ 7 とプロパティ 8 の違いは、両方の方程式の左側で、 X と 1 が入れ替わります。
変数とその補数との組み合わせに関するプロパティ
特性 9: 
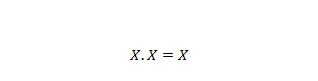
つまり、 X が 0 の場合、 0 になります。 0 = 0。 X が 1 の場合、 1 になります。 1 = 1。
特性 10:
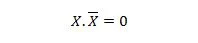
つまり、X が 0 の場合は 0.1 = 0、X が 1 の場合は 1.0 = 0 となります。
連続変数の場合、このプロパティは次のようになります。
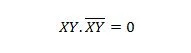
特性 11:
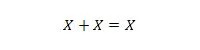
つまり、X が 0 の場合、0 + 0 = 0 になります。X が 1 の場合、1 + 1 = 1 (通常の OR から)。
特性 12:
つまり、X が 0 の場合は 0 + 1 = 1、X = 1 の場合は 1 + 0 = 1 となります。
つまり、X が 0 の場合は 0 + 1 = 1、X = 1 の場合は 1 + 0 = 1 となります。
二重補完
特性 13:
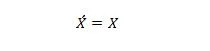
左辺の X が 0 のとき、右辺の X は 0 になります。右辺の X が 1 のとき、左辺の X は 1 になります。つまり、二重補数は元の値を返します。
交換法則
特性 14:
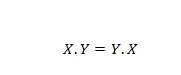
これは、等号の左側にある AND 演算子の最初と 2 番目のオペランドを入れ替えても問題ないことを意味します。左側の交換が行われた後でも、答えは同じです。この方程式は、ドットを省略して XY = YX と書くことができます。
特性 15:
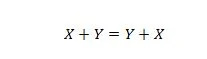
ここでの説明は前の AND と同じですが、OR 演算子についてのものです。
分配法則
特性 16:
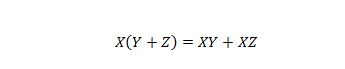
ここには、X、Y、Z の 3 つの変数があります。各変数は 1 または 0 のいずれかです。等号の左側にある括弧は、その中にあるものを最初に評価することを意味します。すると、AND は X との結果になります。右辺は、X と Y の組み合わせ、または X と Z の組み合わせが左辺と同じであることを示しています。 AND のドット演算子はすべて省略されていることに注意してください。そして、結合された変数は依然として AND を意味します。
特性 17:
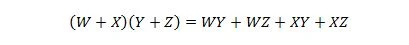
このプロパティは、変数 W が追加されたプロパティ 16 の拡張です。
結合法則
特性 18:
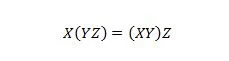
括弧は、括弧内にあるものを最初に評価することを意味します。したがって、左側の式では、最初に Y と Z の AND 演算が行われ、その結果と X の AND 演算が行われる場合、左側の最終結果は右側の最終結果と同じになります。 -hand-side ここでは、結果と Z の AND 演算の前に、最初に X と Y の AND 演算が行われます。方程式ではドットが省略されていることに注意してください。
プロパティ 19:
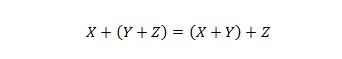
このプロパティはプロパティ 18 と同様の方法で説明されますが、AND 演算子の代わりに OR 演算子が使用されます。簡単にするために、OR 演算子 + がブール式から省略されることはありません。一方、AND 演算子を省略して 2 つの変数を結合することもできます。
吸収
プロパティ 20:
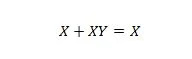
この式では、Y が何であっても、右辺は常に X (吸収) になります。
プロパティ 21:
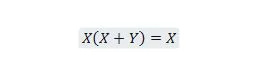
また、この式では、Y が何であっても、右辺は常に X (吸収) になります。このプロパティ 21 は、次のプロパティ 20 と同じです。
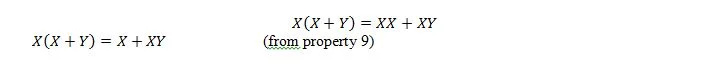
ここでは、分配法則と、性質 9 の X.X = X であるという事実を使用します。
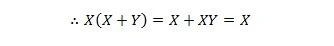
アイデンティティ
プロパティ 22:
これは、X + Y 式の場合、Y の前にある X の補数によって式が変化しないことを意味します。
プロパティ 23:
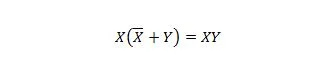
これは、XY 式の場合、X の補数と括弧内の Y の論理和が最初に実行されても、XY 式は変更されないことを意味します。
ドモルガンの法則
プロパティ 24:
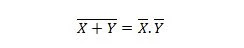
これは、NOR (NOT OR) ゲートが 2 つの入力を AND 演算する前に NOT 演算したのと同じ結果になることを意味します。
プロパティ 25:
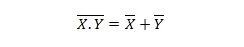
これは、NAND (NOT AND) ゲートが OR 演算の前に 2 つの入力を否定したのと同じ結果になることを意味します。
提供されているイラストは 25 の物件です。これらは、左側の各式に 1 と 0 のさまざまな可能な値をすべて置き換えて、右側の式 (または結果) が得られるかどうかを確認することで証明できます。証明は読者の演習として残されています。
2.5 複合式の簡略化
次の 2 つの関数は同じです。
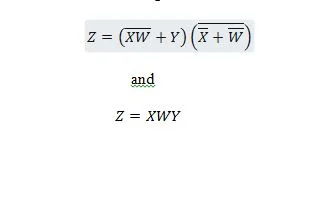
Z は出力、X、W、Y は入力です。最初のゲートには、NAND ゲート、OR ゲート、AND ゲート、2 つの NOT ゲート、OR ゲート、および NOR ゲートが必要です。 2 番目のゲートには 2 つの AND ゲートだけが必要です。最初のものは、右側に複合式を持つ方程式で、2 番目の方程式の単一の右側の式項に簡略化 (縮小) されています。
簡素化または削減すると、回路として同じ機能を実現するためにゲート数が減ります。このような小さな回路は、集積回路 (IC) の一部である場合もあれば、コンピューターのマザーボードの表面にある独立した回路である場合もあります。
関数 (方程式) が設計プロセスに到達すると、ゲート数を減らしてより安価な回路を実現するために単純化を行う必要があります。単純化するには、前述の 25 個のブール特性の 1 つ以上を使用する必要があります。
例 2.51:
方程式を簡略化します。
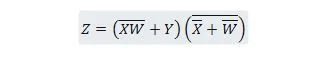
注記： 隣り合う 2 つの括弧は、括弧が AND 演算されていることを意味します (括弧間のドットはオプションで書き込まれません)。
解決：
解決策については、各ステップの正当性 (理由) がステップの右側に括弧内に示されています。読者は各ステップとその正当性を読む必要があります。読者は、関数削減の手順を読むときに、前のプロパティも参照する必要があります。
例 2.52:
簡略化する：
2.6 積の最小合計
次の 2 つの関数は同じです。
両方の方程式の右辺式は、積和 (SP) 形式であると言われます。明示式は、括弧がない場合、Sum of Product 形式であると言われます。最初の関数 (方程式) が 2 番目の関数よりも多くのゲートを必要とすることは明らかです。
最初の右辺式を縮小して 2 番目の関数を取得することもできます。 2 番目の右側の式はこれ以上単純化できず、積の合計 (項の「加算」) として表現できます。 2 番目の右辺の式は、実際にはこれ以上単純化できません。したがって、Minimum Sum of Products (MSP) 形式であると言われます。
例 2.61:
次の関数を最初に積の合計フォームに移動し、次に積の最小合計フォームに移動します。
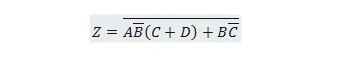
解決：
このような問題を解決する場合、次の解決策に示すように、前の 25 のプロパティのうち 1 つ以上を使用する必要があります。
2.6 積の最小合計
次の 2 つの関数は同じです。
両方の方程式の右辺式は、積和 (SP) 形式であると言われます。明示式は、括弧がない場合、Sum of Product 形式であると言われます。最初の関数 (方程式) が 2 番目の関数よりも多くのゲートを必要とすることは明らかです。
最初の右辺式を縮小して 2 番目の関数を取得することもできます。 2 番目の右側の式はこれ以上単純化できず、積の合計 (項の「加算」) として表現できます。 2 番目の右辺の式は、実際にはこれ以上単純化できません。したがって、Minimum Sum of Products (MSP) 形式であると言われます。
例 2.61:
次の関数を最初に積の合計フォームに移動し、次に積の最小合計フォームに移動します。
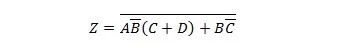
解決：
このような問題を解決する場合、次の解決策に示すように、前の 25 のプロパティのうち 1 つ以上を使用する必要があります。
この最後の式は積和 (SP) 形式ですが、積の最小和 (MSP) 形式ではありません。質問の最初の部分は回答済みです。 2 番目の部分の解決策は次のとおりです。
この最後の単純化された関数 (方程式) は MSP 形式であり、対応する SP 形式よりも実装に必要なゲートの数が少なくなります。覚えておいてください: SP は積の合計を意味し、MSP は積の最小合計を意味します。
例 2.62:
次の回路には X、Y、W 入力があり、Z が出力です。 Z の積和 (SP) 関数 (見かけ上の最小積和関数) を生成します。次に、真のより縮小された (最小化された) 積和 (MSP) を生成します。次に、MSP 回路を実装します (MSP ゲート ネットワークを描画します)。
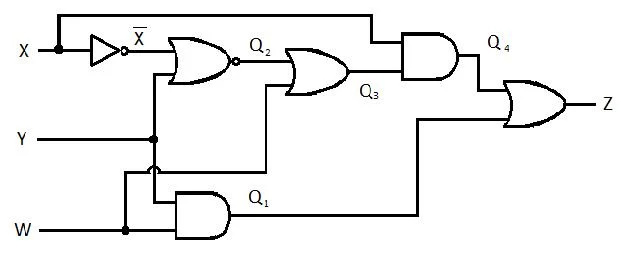
図 2.61 ゲート回路
解決：
単純化プロセスを開始する前に、Z の式を X、Y、および W に関して取得する必要があります。図のこの例を参照してください。
これは、X、Y、および W に関する Z の表現です。この後、見かけの MSP への単純化を行うことができます。見かけ上のMSPはSPです。
この最後の方程式 (関数) は SP 形式です。これは、真の Minimum Sum of Products (まだ MSP ではありません) ではありません。したがって、削減（最小化）を継続する必要があります。
この最後の方程式 (関数) は、真の最小積和 (MSP) です。また、最小積和 (真の最小値) ゲート回路は次のようになります。
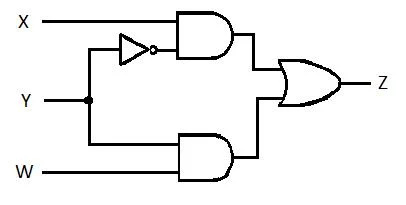
図 2.62 MSP ゲート回路
コメント
このセクションの分析から、積の合計が積の最小合計であるかどうかは明らかではないことがわかります。 SPはあまり役に立ちません。とても便利なのがMSPです。 MSP を確実に入手する方法があります。それはカルノー図を使用することです。カルノー マップは、このオンライン キャリア コースの範囲を超えています。
2.7 問題点
次の章に進む前に、章内のすべての問題を解決することをお勧めします。
- 対応するゲートを使用して AND、OR、NOT 真理値表を作成します。
- 10 個のブール公準をさまざまなカテゴリーに分けて書き留め、カテゴリーに名前を付けます。
- 説明はせずに、ブール代数の 26 の性質をさまざまなカテゴリーに分けて、カテゴリーに名前を付けて書き留めてください。
- ブール値プロパティを使用し、使用されるカテゴリを引用して方程式を簡略化します。
- ブール値プロパティを使用し、使用されるカテゴリを引用して方程式を簡略化します。
- ブール プロパティを使用し、使用されているカテゴリを引用して、次の式を最初に積の合計に、次に積の最小和に縮小します。
- ブール プロパティを使用し、使用されているカテゴリを引用して、次の式を最初に積の合計に、次に積の最小和に縮小します。
